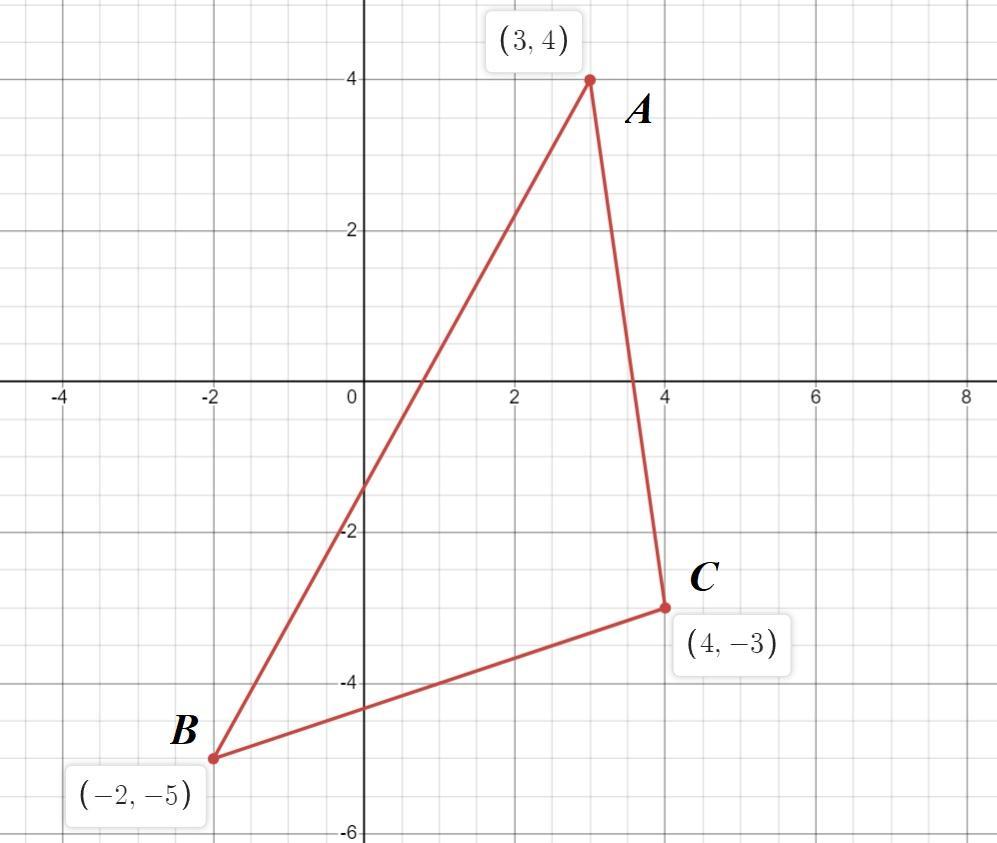
вычислите поверхность треугольника, вершины которого находятся в точках A(3;4), B(-2;-5) и C(4;-3).
Ответ
0
(0 оценок)
0
triolana
1 год назад
Светило науки - 562297 ответов - 388270 раз оказано помощи
Ответ: 33.7 кв. ед.
Объяснение:
вычислите площадь поверхности треугольника, вершины которого находятся в точках A(3;4), B(-2;-5) и C(4;-3).
**********
найдем длины сторон треугольника
a= BC = √((xC-xB)² +(yC-yB)²) =
= √((4-(-2))² + (-3-(-5))²) = √(6²+(-8)²) = √(36+64) = √100 = 10;
b = AC = √((xC-xA)²+ (yC-yA)²) =
= √((4-3)² + (-3-4)²) = √(1²+(-7)²) = √(1+49) = √50 = 5√2;
c= AB = √(xB-xA)² + (yB-yA)² =
=√((-2-3)² + (-5-4)²) = √((-5)²+(-9)²) =√(25+81) = √106;
***********
По формуле Герона
s=√p(p-a)(p-b)(p-c)
p=(a+n+c)/2 = (10+5√2+√106)/2 = 27.37/2 = 13,685 ≈ 13.7;
s = √(13.7(13.7-10)(13.7-5√2)(13.7-√106)) =
= √(13.7*3.7*6.6*3.4) = √1137.5 = 33.7 кв. ед.
Что таакое поверхность треугольника?? Может периметр??