Бічне ребро і висота правильної чотирьохкутної піраміди дорівнює відповідно 12 і 4 см. У піраміду вписано куб так, що його чотири вершини лежать на основі піраміди,а чотири - на апофемах піраміди. Знайти ребро куба (с рисунком)
Ответ
5
(1 оценка)
2
siestarjoki
2 года назад
Светило науки - 2086 ответов - 9766 раз оказано помощи
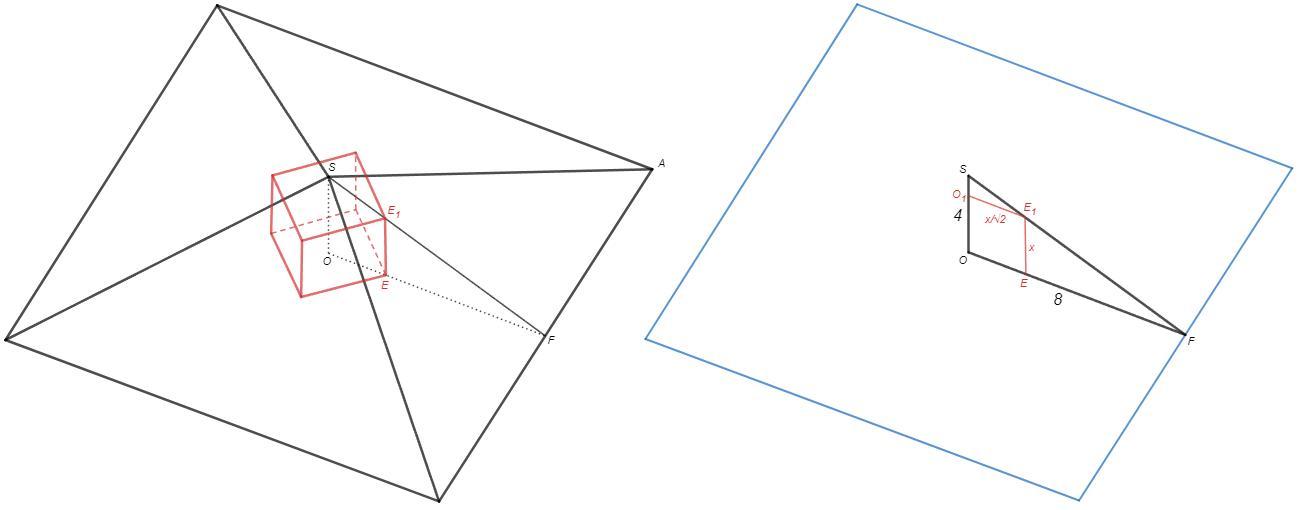
Правильная пирамида, вершина падает в центр основания.
OA =√(SA^2-SO^2) =√(12^2-4^2) =8√2
SF - апофема (высота/медиана боковой грани), OF=8
Из симметрии следует, что пирамида и куб имеют общую ось.
Высота SO проходит через центры оснований куба O и O1.
EE1=x (ребро куба)
OE=O1E1=x/√2 (половина диагонали основания куба)
SO/OF =SO1/O1E1 =>
4/8 =(4-x)/ x/√2 => x =8√2/(1+2√2) =8(4-√2)/7 (см)
8(4-√2)/7
а решение с рисунком можно?
да, через час